\[ \begin{align}\begin{aligned}\newcommand\blank{~\underline{\hspace{1.2cm}}~}\\% Bold symbols (vectors)
\newcommand\bs[1]{\mathbf{#1}}\\% Differential
\newcommand\dd[2][]{\mathrm{d}^{#1}{#2}} % use as \dd, \dd{x}, or \dd[2]{x}\\% Poor man's siunitx
\newcommand\unit[1]{\mathrm{#1}}
\newcommand\num[1]{#1}
\newcommand\qty[2]{#1~\unit{#2}}\\\newcommand\per{/}
\newcommand\squared{{}^2}
\newcommand\cubed{{}^3}
%
% Scale
\newcommand\milli{\unit{m}}
\newcommand\centi{\unit{c}}
\newcommand\kilo{\unit{k}}
\newcommand\mega{\unit{M}}
%
% Percent
\newcommand\percent{\unit{\%}}
%
% Angle
\newcommand\radian{\unit{rad}}
\newcommand\degree{\unit{{}^\circ}}
%
% Time
\newcommand\second{\unit{s}}
\newcommand\s{\second}
\newcommand\minute{\unit{min}}
\newcommand\hour{\unit{h}}
%
% Distance
\newcommand\meter{\unit{m}}
\newcommand\m{\meter}
\newcommand\inch{\unit{in}}
\newcommand\foot{\unit{ft}}
%
% Force
\newcommand\newton{\unit{N}}
\newcommand\kip{\unit{kip}} % kilopound in "freedom" units - edit made by Sri
%
% Mass
\newcommand\gram{\unit{g}}
\newcommand\g{\gram}
\newcommand\kilogram{\unit{kg}}
\newcommand\kg{\kilogram}
\newcommand\grain{\unit{grain}}
\newcommand\ounce{\unit{oz}}
%
% Temperature
\newcommand\kelvin{\unit{K}}
\newcommand\K{\kelvin}
\newcommand\celsius{\unit{{}^\circ C}}
\newcommand\C{\celsius}
\newcommand\fahrenheit{\unit{{}^\circ F}}
\newcommand\F{\fahrenheit}
%
% Area
\newcommand\sqft{\unit{sq\,\foot}} % square foot
%
% Volume
\newcommand\liter{\unit{L}}
\newcommand\gallon{\unit{gal}}
%
% Frequency
\newcommand\hertz{\unit{Hz}}
\newcommand\rpm{\unit{rpm}}
%
% Voltage
\newcommand\volt{\unit{V}}
\newcommand\V{\volt}
\newcommand\millivolt{\milli\volt}
\newcommand\mV{\milli\volt}
\newcommand\kilovolt{\kilo\volt}
\newcommand\kV{\kilo\volt}
%
% Current
\newcommand\ampere{\unit{A}}
\newcommand\A{\ampere}
\newcommand\milliampereA{\milli\ampere}
\newcommand\mA{\milli\ampere}
\newcommand\kiloampereA{\kilo\ampere}
\newcommand\kA{\kilo\ampere}
%
% Resistance
\newcommand\ohm{\Omega}
\newcommand\milliohm{\milli\ohm}
\newcommand\kiloohm{\kilo\ohm} % correct SI spelling
\newcommand\kilohm{\kilo\ohm} % "American" spelling used in siunitx
\newcommand\megaohm{\mega\ohm} % correct SI spelling
\newcommand\megohm{\mega\ohm} % "American" spelling used in siunitx
%
% Inductance
\newcommand\henry{\unit{H}}
\newcommand\H{\henry}
\newcommand\millihenry{\milli\henry}
\newcommand\mH{\milli\henry}
%
% Power
\newcommand\watt{\unit{W}}
\newcommand\W{\watt}
\newcommand\milliwatt{\milli\watt}
\newcommand\mW{\milli\watt}
\newcommand\kilowatt{\kilo\watt}
\newcommand\kW{\kilo\watt}
%
% Energy
\newcommand\joule{\unit{J}}
\newcommand\J{\joule}
%
% Composite units
%
% Torque
\newcommand\ozin{\unit{\ounce}\,\unit{in}}
\newcommand\newtonmeter{\unit{\newton\,\meter}}
%
% Pressure
\newcommand\psf{\unit{psf}} % pounds per square foot
\newcommand\pcf{\unit{pcf}} % pounds per cubic foot
\newcommand\pascal{\unit{Pa}}
\newcommand\Pa{\pascal}
\newcommand\ksi{\unit{ksi}} % kilopound per square inch
\newcommand\bar{\unit{bar}}
\end{aligned}\end{align} \]
Mar 14, 2025 | 257 words | 3 min read
7.2.3. Task 3
Learning Objectives
Read and interpret a flowchart that contains user-defined functions; Design a program
with user-defined functions; Understand the execution sequence for a program with
user-defined functions.
Introduction
As the scripts and programs we write become more complex, we often do not want to put
all of our code directly in the main Python allows users
to easily write their own functions in order to modularize their programs; these are
called user-defined functions.
Task Instructions
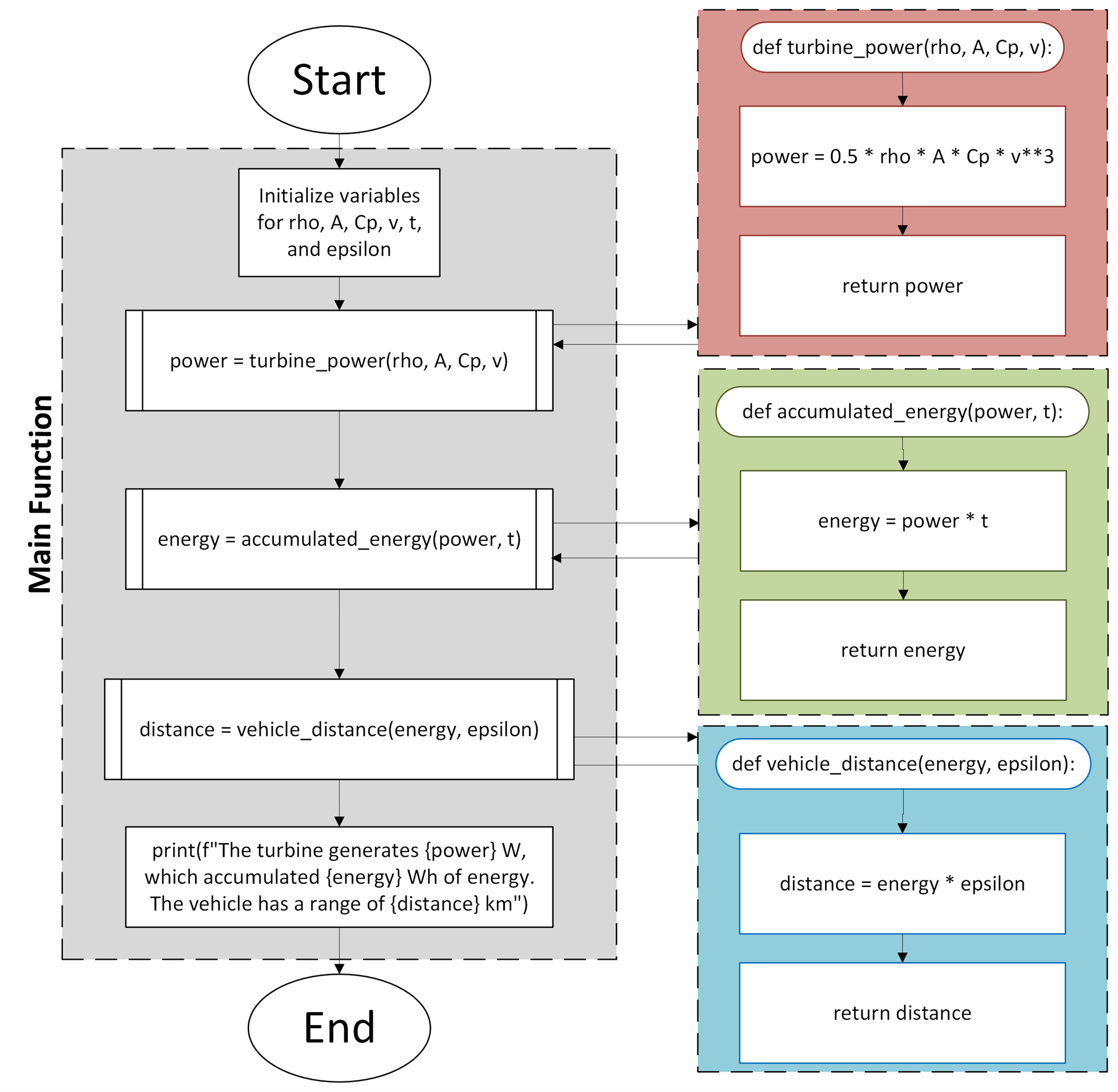
Your team is designing an electric vehicle that will be charged by a wind turbine. You
want to write a program that gives a rough estimate for how far the vehicle can travel
after a given amount of charging time. A flowchart for that program is shown in
Fig. 7.1
The power of the wind turbine is given by:
(7.1) \[P = \frac{1}{2} \rho A v^3 C_p\]
Where
\(P\) is the power
\(\rho\) is the air density
\(A\) is the rotor swept area
\(v\) is the wind velocity
\(C_p\) is a coefficient of efficiency
The energy in the car is given by:
(7.2) \[E = Pt\]
Where
E is the energy
P is the power
t is the time
The distance that an electric vehicle can travel is given by:
(7.3) \[d = E\epsilon_v\]
Where
Note: Convert the distance from m to km before printing to the terminal. This can be done using simple division in Python .
Fig. 7.1 Flowchart for Team Task 3
Save your answers to a PDF named py1_team_teamnumber.pdf .