\[ \begin{align}\begin{aligned}\newcommand\blank{~\underline{\hspace{1.2cm}}~}\\% Bold symbols (vectors) \newcommand\bs[1]{\mathbf{#1}}\\% Differential \newcommand\dd[2][]{\mathrm{d}^{#1}{#2}} % use as \dd, \dd{x}, or \dd[2]{x}\\% Poor man's siunitx \newcommand\unit[1]{\mathrm{#1}} \newcommand\num[1]{#1} \newcommand\qty[2]{#1~\unit{#2}}\\\newcommand\per{/} \newcommand\squared{{}^2} \newcommand\cubed{{}^3} % % Scale \newcommand\milli{\unit{m}} \newcommand\centi{\unit{c}} \newcommand\kilo{\unit{k}} \newcommand\mega{\unit{M}} % % Percent \newcommand\percent{\unit{{\kern-4mu}\%}} % % Angle \newcommand\radian{\unit{rad}} \newcommand\degree{\unit{{\kern-4mu}^\circ}} % % Time \newcommand\second{\unit{s}} \newcommand\s{\second} \newcommand\minute{\unit{min}} \newcommand\hour{\unit{h}} % % Distance \newcommand\meter{\unit{m}} \newcommand\m{\meter} \newcommand\inch{\unit{in}} \newcommand\foot{\unit{ft}} % % Force \newcommand\newton{\unit{N}} \newcommand\kip{\unit{kip}} % kilopound in "freedom" units - edit made by Sri % % Mass \newcommand\gram{\unit{g}} \newcommand\g{\gram} \newcommand\kilogram{\unit{kg}} \newcommand\kg{\kilogram} \newcommand\grain{\unit{grain}} \newcommand\ounce{\unit{oz}} % % Temperature \newcommand\kelvin{\unit{K}} \newcommand\K{\kelvin} \newcommand\celsius{\unit{{}^\circ C}} \newcommand\C{\celsius} \newcommand\fahrenheit{\unit{{}^\circ F}} \newcommand\F{\fahrenheit} % % Area \newcommand\sqft{\unit{sq\,\foot}} % square foot % % Volume \newcommand\liter{\unit{L}} \newcommand\gallon{\unit{gal}} % % Frequency \newcommand\hertz{\unit{Hz}} \newcommand\rpm{\unit{rpm}} % % Voltage \newcommand\volt{\unit{V}} \newcommand\V{\volt} \newcommand\millivolt{\milli\volt} \newcommand\mV{\milli\volt} \newcommand\kilovolt{\kilo\volt} \newcommand\kV{\kilo\volt} % % Current \newcommand\ampere{\unit{A}} \newcommand\A{\ampere} \newcommand\milliampereA{\milli\ampere} \newcommand\mA{\milli\ampere} \newcommand\kiloampereA{\kilo\ampere} \newcommand\kA{\kilo\ampere} % % Resistance \newcommand\ohm{\Omega} \newcommand\milliohm{\milli\ohm} \newcommand\kiloohm{\kilo\ohm} % correct SI spelling \newcommand\kilohm{\kilo\ohm} % "American" spelling used in siunitx \newcommand\megaohm{\mega\ohm} % correct SI spelling \newcommand\megohm{\mega\ohm} % "American" spelling used in siunitx % % Capacitance \newcommand\farad{\unit{F}} \newcommand\F{\farad} \newcommand\microfarad{\micro\farad} \newcommand\muF{\micro\farad} % % Inductance \newcommand\henry{\unit{H}} \newcommand\H{\henry} \newcommand\millihenry{\milli\henry} \newcommand\mH{\milli\henry} % % Power \newcommand\watt{\unit{W}} \newcommand\W{\watt} \newcommand\milliwatt{\milli\watt} \newcommand\mW{\milli\watt} \newcommand\kilowatt{\kilo\watt} \newcommand\kW{\kilo\watt} % % Energy \newcommand\joule{\unit{J}} \newcommand\J{\joule} % % Composite units % % Torque \newcommand\ozin{\unit{\ounce}\,\unit{in}} \newcommand\newtonmeter{\unit{\newton\,\meter}} % % Pressure \newcommand\psf{\unit{psf}} % pounds per square foot \newcommand\pcf{\unit{pcf}} % pounds per cubic foot \newcommand\pascal{\unit{Pa}} \newcommand\Pa{\pascal} \newcommand\ksi{\unit{ksi}} % kilopound per square inch \newcommand\bar{\unit{bar}} \end{aligned}\end{align} \]

Jan 19, 2026 | 349 words | 3 min read

12.2.3. Task 3

Learning Objectives

Read and interpret a flowchart that contains user-defined functions; Design a program with user-defined functions; Investigate the advantages of user-defined functions in Python;

Introduction

You find yourself stranded on an unknown planet. As an aspiring engineer, you decide to design a rocket capable of escaping the planet’s gravitational pull so you can return home. To do this, you must write a program that calculates the minimum velocity, known as escape velocity, required for your rocket to break free from the planet’s gravitational field.

The escape velocity of an object is given by

(12.3)\[v_e = \sqrt{\frac{2\,G\,m}{r}},\]

where

• \(v_e\) is the escape velocity

• \(G\) is the gravitational constant (\(\qty{6.6743 \times 10^{-11}}{\meter^{3}\per\kilo\gram\cdot\second\squared}\))

• \(m\) is the mass of the planet, and

• \(r\) is the radius of the planet

The mass of the planet is given by

(12.4)\[m = \rho \, V,\]

where

• \(\rho\) is the planet’s average density and

• \(V\) is the volume.

Assuming the planet is spherical, its volume is given by

(12.5)\[V = \frac{4}{3} \, \pi \, r^{3},\]

where

• r is the radius.

Task Instructions

Following the flowchart in Fig. 12.1, write a Python program with three user-defined functions and a main function that calculates the minimum velocity required for your rocket to break free from the planet’s gravitational field. Your main function should initialize the gravitational constant and then prompt the user for the planet’s average density and radius, before calling each of the user-defined functions in turn and then displaying the results.

In the calc_escape_velocity function, check that the radius and mass are positive. If they are negative, print an error message as shown in the test cases, and return \(0\) as the escape velocity. Otherwise, calculate and return the escape velocity.

Note

The radius is converted from \(\meter\) to \(\kilo\meter\) before printing to the terminal.

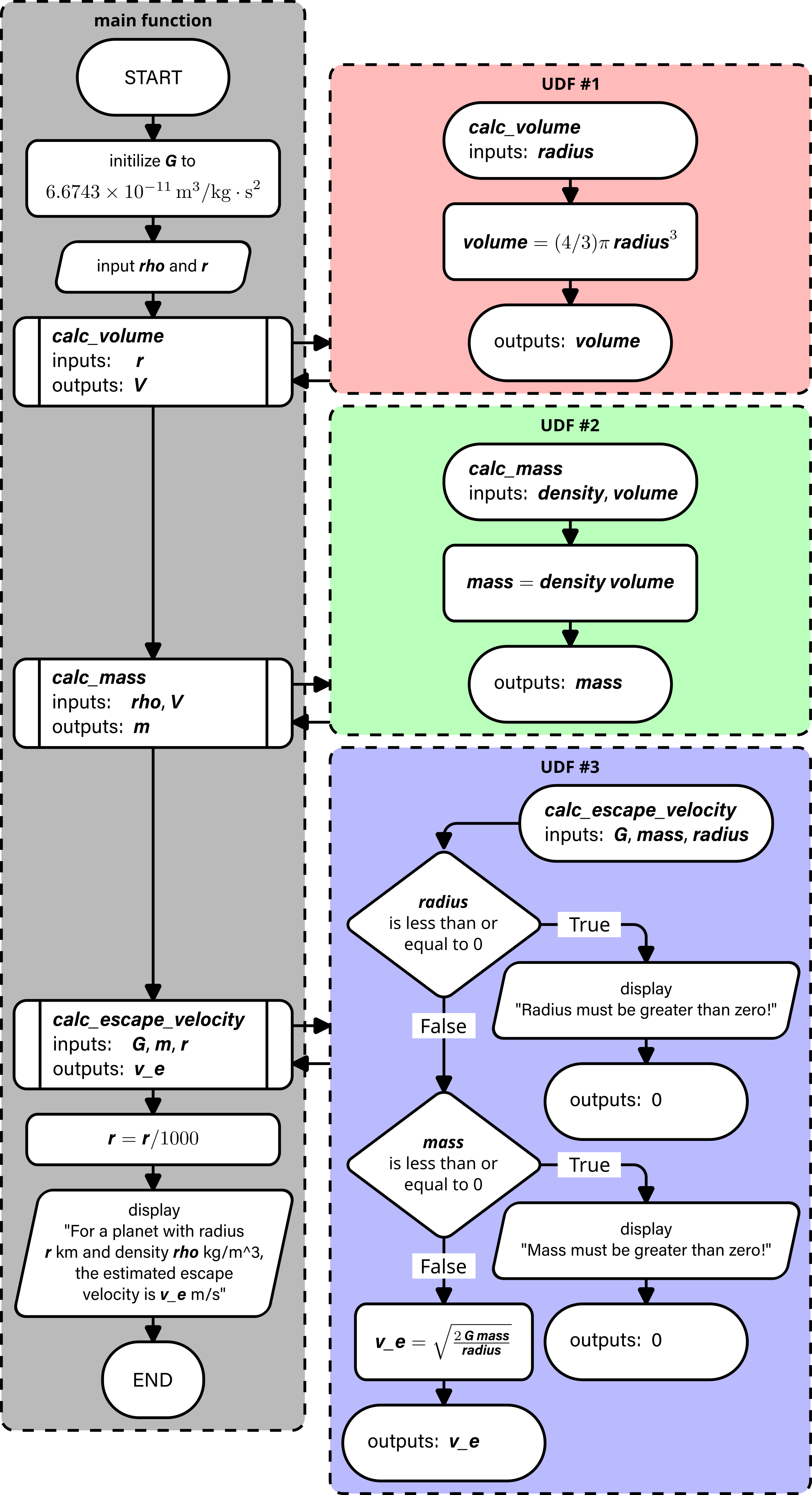
Fig. 12.1 Escape velocity program flowchart.

Sample Output

Use the values in Table 12.6 below to test your program.

Table 12.6 Test Cases

Case	\(\rho\) (\(\frac{\kilo\gram}{\meter^3}\))	Radius (\(\meter\))
1	5513.0	6371000
2	1879.8	2574730
3	300.0	-600.0
4	-4200	6310100

Ensure your program’s output matches the provided samples exactly. This includes all characters, white space, and punctuation. In the samples, user input is highlighted like this for clarity, but your program should not highlight user input in this way.

Case 1 Sample Output

$ python3 py2_team_3_main_teamnumber.py Enter the average density of the planet: 5513.0 Enter the radius of the planet: 6371000 For a planet with radius 6,371.0 km and density 5,513.00 kg/m^3, the estimated escape velocity is 11,185.72 m/s

Case 2 Sample Output

$ python3 py2_team_3_main_teamnumber.py Enter the average density of the planet: 1879.8 Enter the radius of the planet: 2574730 For a planet with radius 2,574.7 km and density 1,879.80 kg/m^3, the estimated escape velocity is 2,639.67 m/s

Case 3 Sample Output

$ python3 py2_team_3_main_teamnumber.py Enter the average density of the planet: 300.0 Enter the radius of the planet: -600.0 Radius must be greater than zero! For a planet with radius -0.6 km and density 300.00 kg/m^3, the estimated escape velocity is 0.00 m/s

Case 4 Sample Output

$ python3 py2_team_3_main_teamnumber.py Enter the average density of the planet: -4200 Enter the radius of the planet: 6310100 Mass must be greater than zero! For a planet with radius 6,310.1 km and density -4,200.00 kg/m^3, the estimated escape velocity is 0.00 m/s

Table 12.7 Deliverables

Deliverables	Description
py2_team_3_mass_teamnumber.py	Your completed mass calculation function.
py2_team_3_volume_teamnumber.py	Your completed volume calculation function.
py2_team_3_escape_velocity_teamnumber.py	Your completed escape velocity function.
py2_team_3_main_teamnumber.py	Your completed main Python code.