\[ \begin{align}\begin{aligned}\newcommand\blank{~\underline{\hspace{1.2cm}}~}\\% Bold symbols (vectors)
\newcommand\bs[1]{\mathbf{#1}}\\% Differential
\newcommand\dd[2][]{\mathrm{d}^{#1}{#2}} % use as \dd, \dd{x}, or \dd[2]{x}\\% Poor man's siunitx
\newcommand\unit[1]{\mathrm{#1}}
\newcommand\num[1]{#1}
\newcommand\qty[2]{#1~\unit{#2}}\\\newcommand\per{/}
\newcommand\squared{{}^2}
\newcommand\cubed{{}^3}
%
% Scale
\newcommand\milli{\unit{m}}
\newcommand\centi{\unit{c}}
\newcommand\kilo{\unit{k}}
\newcommand\mega{\unit{M}}
%
% Percent
\newcommand\percent{\unit{{\kern-4mu}\%}}
%
% Angle
\newcommand\radian{\unit{rad}}
\newcommand\degree{\unit{{\kern-4mu}^\circ}}
%
% Time
\newcommand\second{\unit{s}}
\newcommand\s{\second}
\newcommand\minute{\unit{min}}
\newcommand\hour{\unit{h}}
%
% Distance
\newcommand\meter{\unit{m}}
\newcommand\m{\meter}
\newcommand\inch{\unit{in}}
\newcommand\foot{\unit{ft}}
%
% Force
\newcommand\newton{\unit{N}}
\newcommand\kip{\unit{kip}} % kilopound in "freedom" units - edit made by Sri
%
% Mass
\newcommand\gram{\unit{g}}
\newcommand\g{\gram}
\newcommand\kilogram{\unit{kg}}
\newcommand\kg{\kilogram}
\newcommand\grain{\unit{grain}}
\newcommand\ounce{\unit{oz}}
%
% Temperature
\newcommand\kelvin{\unit{K}}
\newcommand\K{\kelvin}
\newcommand\celsius{\unit{{}^\circ C}}
\newcommand\C{\celsius}
\newcommand\fahrenheit{\unit{{}^\circ F}}
\newcommand\F{\fahrenheit}
%
% Area
\newcommand\sqft{\unit{sq\,\foot}} % square foot
%
% Volume
\newcommand\liter{\unit{L}}
\newcommand\gallon{\unit{gal}}
%
% Frequency
\newcommand\hertz{\unit{Hz}}
\newcommand\rpm{\unit{rpm}}
%
% Voltage
\newcommand\volt{\unit{V}}
\newcommand\V{\volt}
\newcommand\millivolt{\milli\volt}
\newcommand\mV{\milli\volt}
\newcommand\kilovolt{\kilo\volt}
\newcommand\kV{\kilo\volt}
%
% Current
\newcommand\ampere{\unit{A}}
\newcommand\A{\ampere}
\newcommand\milliampereA{\milli\ampere}
\newcommand\mA{\milli\ampere}
\newcommand\kiloampereA{\kilo\ampere}
\newcommand\kA{\kilo\ampere}
%
% Resistance
\newcommand\ohm{\Omega}
\newcommand\milliohm{\milli\ohm}
\newcommand\kiloohm{\kilo\ohm} % correct SI spelling
\newcommand\kilohm{\kilo\ohm} % "American" spelling used in siunitx
\newcommand\megaohm{\mega\ohm} % correct SI spelling
\newcommand\megohm{\mega\ohm} % "American" spelling used in siunitx
%
% Capacitance
\newcommand\farad{\unit{F}}
\newcommand\F{\farad}
\newcommand\microfarad{\micro\farad}
\newcommand\muF{\micro\farad}
%
% Inductance
\newcommand\henry{\unit{H}}
\newcommand\H{\henry}
\newcommand\millihenry{\milli\henry}
\newcommand\mH{\milli\henry}
%
% Power
\newcommand\watt{\unit{W}}
\newcommand\W{\watt}
\newcommand\milliwatt{\milli\watt}
\newcommand\mW{\milli\watt}
\newcommand\kilowatt{\kilo\watt}
\newcommand\kW{\kilo\watt}
%
% Energy
\newcommand\joule{\unit{J}}
\newcommand\J{\joule}
%
% Composite units
%
% Torque
\newcommand\ozin{\unit{\ounce}\,\unit{in}}
\newcommand\newtonmeter{\unit{\newton\,\meter}}
%
% Pressure
\newcommand\psf{\unit{psf}} % pounds per square foot
\newcommand\pcf{\unit{pcf}} % pounds per cubic foot
\newcommand\pascal{\unit{Pa}}
\newcommand\Pa{\pascal}
\newcommand\ksi{\unit{ksi}} % kilopound per square inch
\newcommand\bar{\unit{bar}}
\end{aligned}\end{align} \]
Dec 04, 2025 | 281 words | 3 min read
7.2.3. Task 3
Learning Objectives
Read and interpret a flowchart that contains user-defined functions; Design a program
with user-defined functions; Understand the execution sequence for a program with
user-defined functions.
Introduction
As the scripts and programs we write become more complex, we often do not want to put
all of our code directly in the main Python allows users
to easily write their own functions in order to modularize their programs; these are
called user-defined functions.
Task Instructions
You find yourself abandoned on an unknown planet. However, since you are an aspiring
engineer, you plan to design a rocket cable of getting you back home. As part of this,
you need to write a program that estimates the minimum velocity your rocket must achieve
to escape the gravitational field of this mystery planet. Commonly known as the escape
velocity. You however, are only aware of the average density of the planet and its
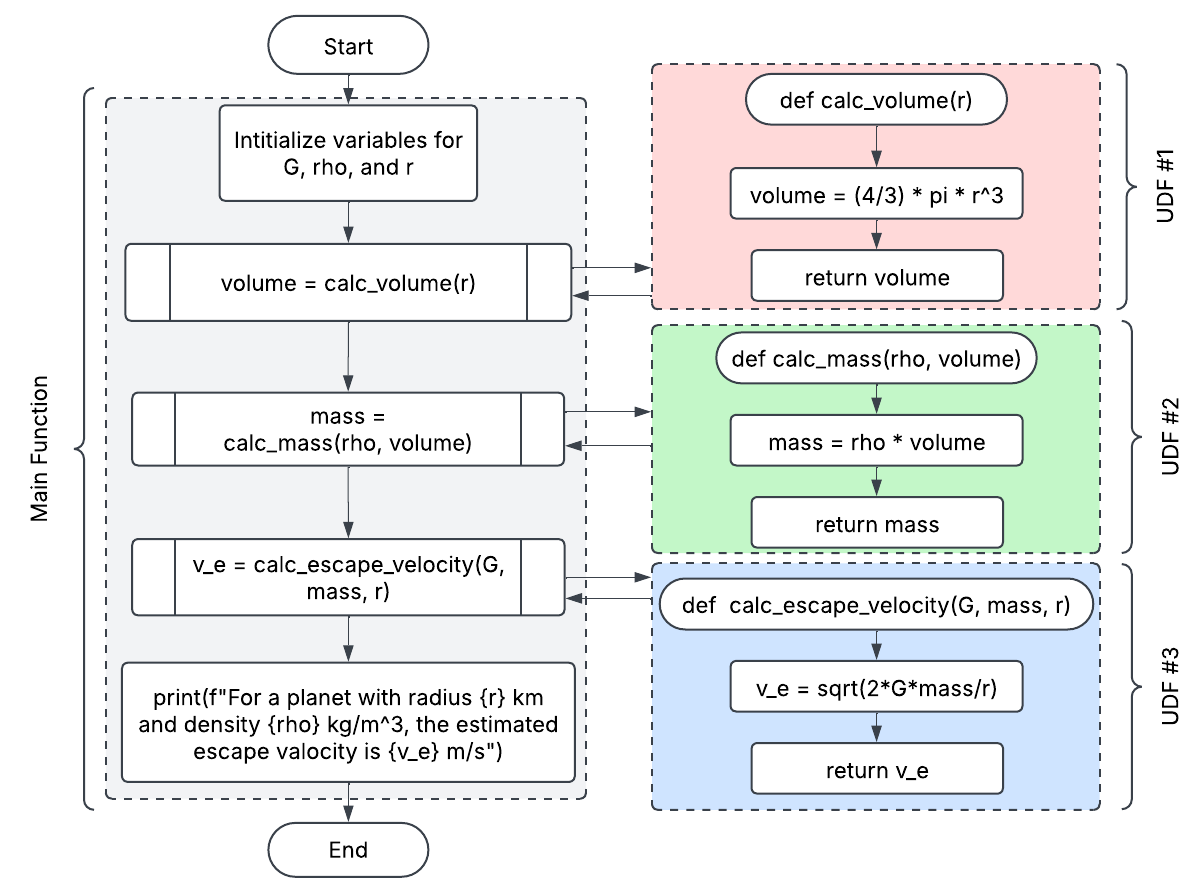
radius. A flowchart for that program is shown in Fig. 7.1
The escape velocity of a projectile is given by:
(7.1) \[v_e = \sqrt{\frac{2Gm}{r}}\]
Where
\(v_e\) is the escape velocity
\(G\) is the gravitational constant
\(m\) is the mass of the planet
\(r\) is the radius of the planet
The mass of the planet is given by:
(7.2) \[m = \rho \times V\]
Where
The volume of a sphere is given by (we approximate the planet’s shape to be a sphere):
(7.3) \[V = \frac{4}{3}\times\pi\times r^{3}\]
Where
Note
Convert the radius from m to km before printing to the terminal. This can be done using simple division in Python
Fig. 7.1 Flowchart for Team Task 3
Save your answers to a PDF named py1_team_3_teamnumber.pdf .