\[ \begin{align}\begin{aligned}\newcommand\blank{~\underline{\hspace{1.2cm}}~}\\% Bold symbols (vectors) \newcommand\bs[1]{\mathbf{#1}}\\% Differential \newcommand\dd[2][]{\mathrm{d}^{#1}{#2}} % use as \dd, \dd{x}, or \dd[2]{x}\\% Poor man's siunitx \newcommand\unit[1]{\mathrm{#1}} \newcommand\num[1]{#1} \newcommand\qty[2]{#1~\unit{#2}}\\\newcommand\per{/} \newcommand\squared{{}^2} \newcommand\cubed{{}^3} % % Scale \newcommand\milli{\unit{m}} \newcommand\centi{\unit{c}} \newcommand\kilo{\unit{k}} \newcommand\mega{\unit{M}} % % Percent \newcommand\percent{\unit{{\kern-4mu}\%}} % % Angle \newcommand\radian{\unit{rad}} \newcommand\degree{\unit{{\kern-4mu}^\circ}} % % Time \newcommand\second{\unit{s}} \newcommand\s{\second} \newcommand\minute{\unit{min}} \newcommand\hour{\unit{h}} % % Distance \newcommand\meter{\unit{m}} \newcommand\m{\meter} \newcommand\inch{\unit{in}} \newcommand\foot{\unit{ft}} % % Force \newcommand\newton{\unit{N}} \newcommand\kip{\unit{kip}} % kilopound in "freedom" units - edit made by Sri % % Mass \newcommand\gram{\unit{g}} \newcommand\g{\gram} \newcommand\kilogram{\unit{kg}} \newcommand\kg{\kilogram} \newcommand\grain{\unit{grain}} \newcommand\ounce{\unit{oz}} % % Temperature \newcommand\kelvin{\unit{K}} \newcommand\K{\kelvin} \newcommand\celsius{\unit{{}^\circ C}} \newcommand\C{\celsius} \newcommand\fahrenheit{\unit{{}^\circ F}} \newcommand\F{\fahrenheit} % % Area \newcommand\sqft{\unit{sq\,\foot}} % square foot % % Volume \newcommand\liter{\unit{L}} \newcommand\gallon{\unit{gal}} % % Frequency \newcommand\hertz{\unit{Hz}} \newcommand\rpm{\unit{rpm}} % % Voltage \newcommand\volt{\unit{V}} \newcommand\V{\volt} \newcommand\millivolt{\milli\volt} \newcommand\mV{\milli\volt} \newcommand\kilovolt{\kilo\volt} \newcommand\kV{\kilo\volt} % % Current \newcommand\ampere{\unit{A}} \newcommand\A{\ampere} \newcommand\milliampereA{\milli\ampere} \newcommand\mA{\milli\ampere} \newcommand\kiloampereA{\kilo\ampere} \newcommand\kA{\kilo\ampere} % % Resistance \newcommand\ohm{\Omega} \newcommand\milliohm{\milli\ohm} \newcommand\kiloohm{\kilo\ohm} % correct SI spelling \newcommand\kilohm{\kilo\ohm} % "American" spelling used in siunitx \newcommand\megaohm{\mega\ohm} % correct SI spelling \newcommand\megohm{\mega\ohm} % "American" spelling used in siunitx % % Capacitance \newcommand\farad{\unit{F}} \newcommand\F{\farad} \newcommand\microfarad{\micro\farad} \newcommand\muF{\micro\farad} % % Inductance \newcommand\henry{\unit{H}} \newcommand\H{\henry} \newcommand\millihenry{\milli\henry} \newcommand\mH{\milli\henry} % % Power \newcommand\watt{\unit{W}} \newcommand\W{\watt} \newcommand\milliwatt{\milli\watt} \newcommand\mW{\milli\watt} \newcommand\kilowatt{\kilo\watt} \newcommand\kW{\kilo\watt} % % Energy \newcommand\joule{\unit{J}} \newcommand\J{\joule} % % Composite units % % Torque \newcommand\ozin{\unit{\ounce}\,\unit{in}} \newcommand\newtonmeter{\unit{\newton\,\meter}} % % Pressure \newcommand\psf{\unit{psf}} % pounds per square foot \newcommand\pcf{\unit{pcf}} % pounds per cubic foot \newcommand\pascal{\unit{Pa}} \newcommand\Pa{\pascal} \newcommand\ksi{\unit{ksi}} % kilopound per square inch \newcommand\bar{\unit{bar}} \end{aligned}\end{align} \]

Dec 04, 2025 | 1006 words | 10 min read

12.2.2. Task 2

Learning Objectives

• Implement a Sobel Filter from scratch

• Understand how thresholding is used in Sobel filtering

Task Instructions

Save the flowcharts for this task in tp2_team_2_teamnumber.pdf You will also need to include these flowcharts in your final report.

Write a function named sobel_filter to identify the edges of an image. Name this program tp2_team_2_teamnumber.py.

How do we find the edges in an image ?

Now that we have blurred the images using the Gaussian filter from Section 12.2.1 we will be constructing a Sobel filter to highlight the edges within the blurred image.

The Sobel filter works by passing the image through 2 different Sobel kernels (one for the \(x\) direction and one for the \(y\) direction). These kernels work in the same way that the Gaussian kernel worked in the previous task, but the values are chosen in such a way as to calculate what is called the gradient in the respective direction.

You can think of the gradient as the measure of slope in the pixel values in a given direction. To illustrate how these kernels actually behave on an image let’s start with a horizontal and vertical line demonstration :

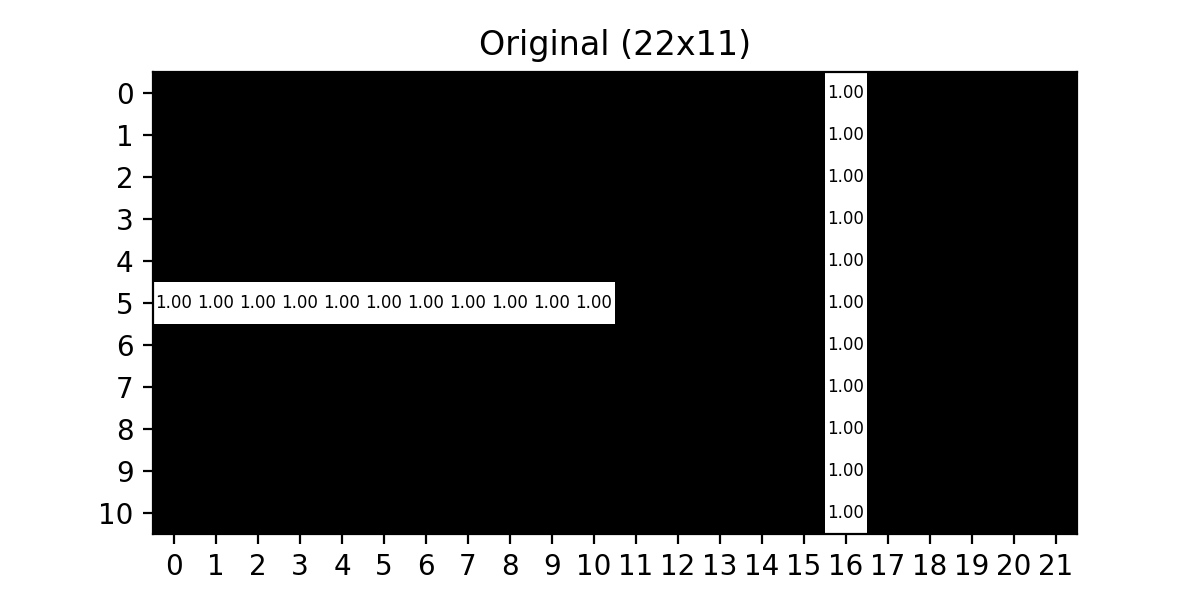
Fig. 12.10 Original 22x11 Horizontal / Vertical

We will now apply the \(\text{Sobel}_x\) kernel to show the gradient in the \(x\) direction :

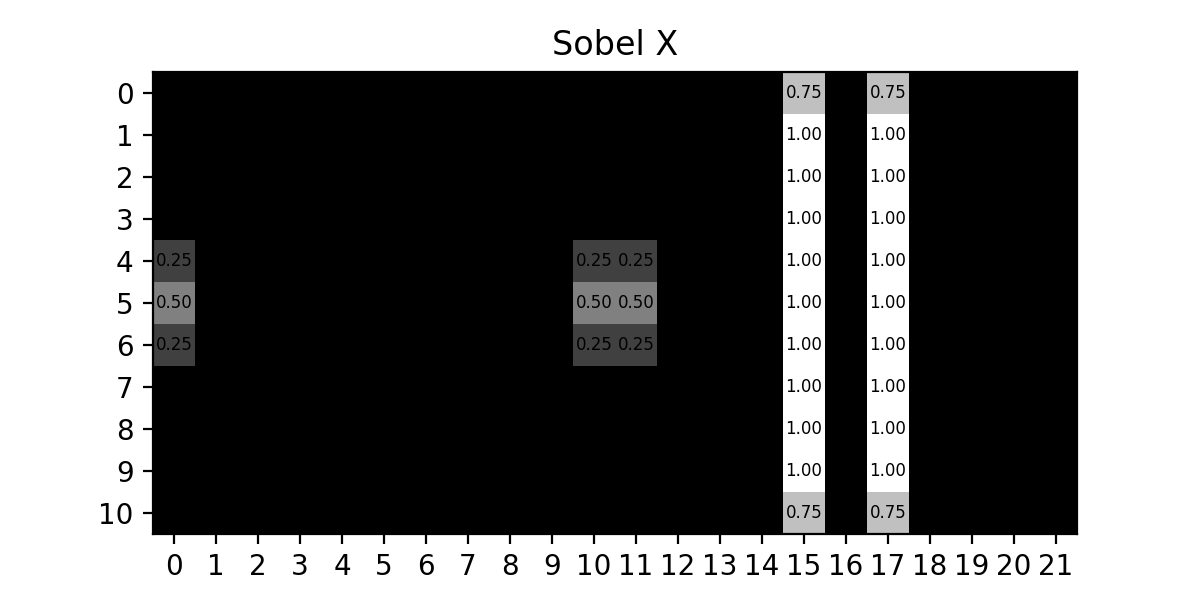
Fig. 12.11 Sobel X Kernel

Since this filter should only highlight the areas where the pixels change from left to right it makes sense that the horizontal line essentially disappears (except for where it starts and stops) while the edges of the original vertical line are emphasized.

Applying the \(\text{Sobel}_y\) kernel to the original image, we should see the areas where pixels change from top to bottom :

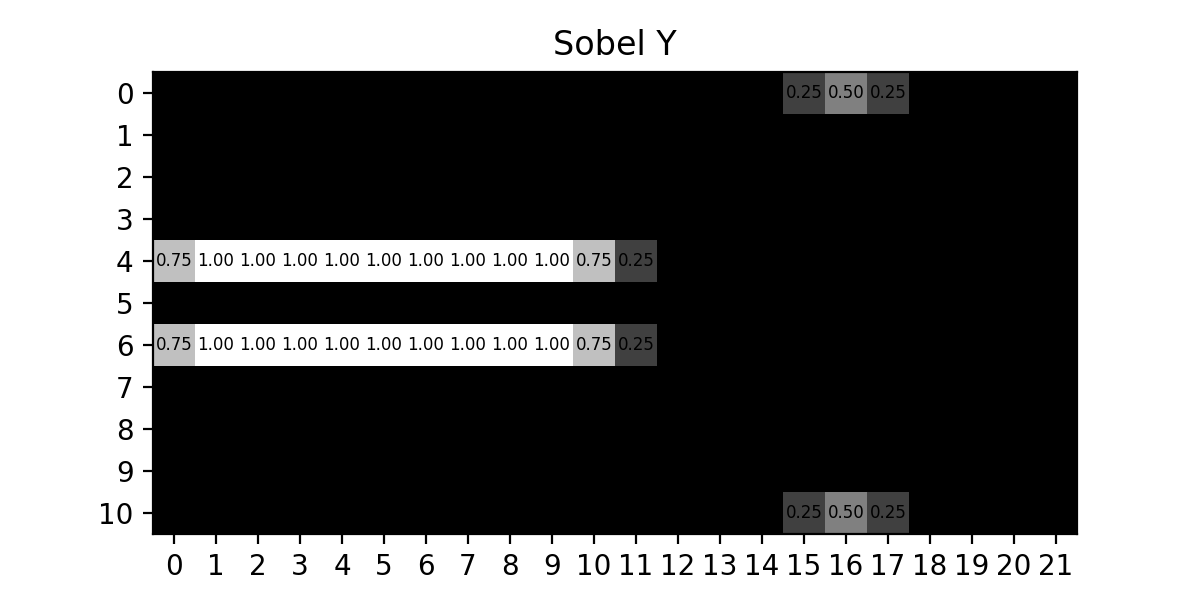
Fig. 12.12 Sobel Y Kernel

As we can see, each of the kernels are able to highlight the changes in their respective directions, so in order to find all the edges in an image we simply need to combine these results, which gives us :

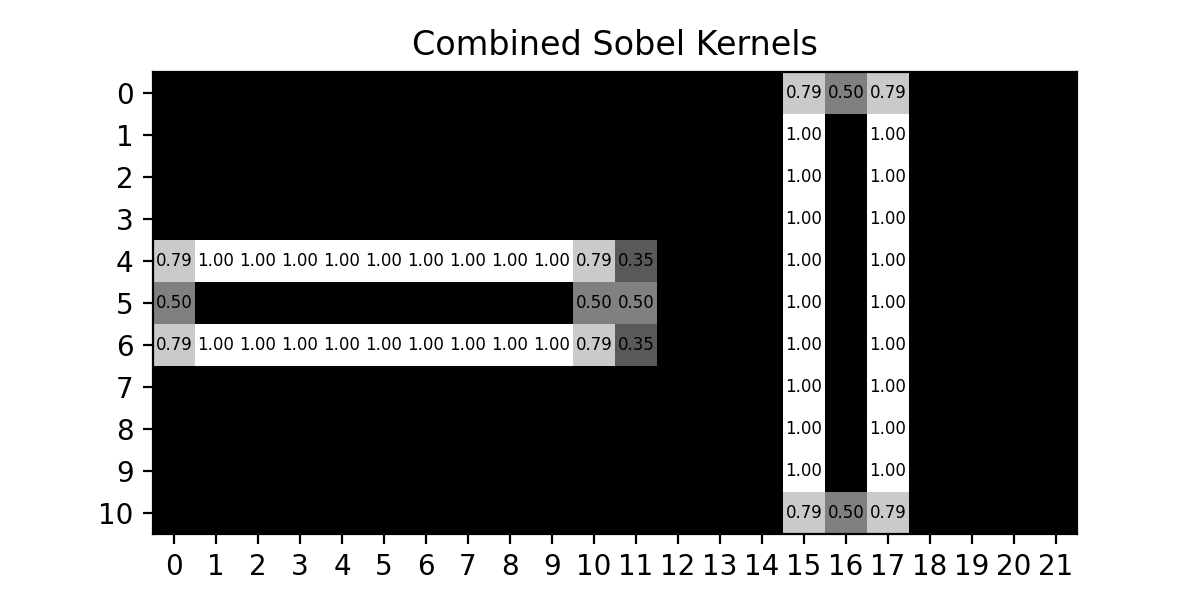
Fig. 12.13 Combined Sobel Kernels

Note

This is ONLY the output of combining the two Sobel kernels’ outputs. A Sobel filter would still have the final step of pixel thresholding so that all pixels would be either white or black indicating whether that pixel IS or IS NOT an edge.

How do we construct the Sobel filter ?

The Sobel filter starts with the two, directional kernels, \(\text{Sobel}_x\) and \(\text{Sobel}_y\), which are defined as follows :

\[\begin{split} \text{Sobel}_x = \left(\begin{array}{cc} -1& 0& 1 \\ -2& 0& 2 \\ -1& 0& 1 \end{array}\right) \quad \text{Sobel}_y = \left(\begin{array}{c} -1& -2& -1 \\ 0& 0& 0 \\ 1& 2& 1 \end{array}\right) \end{split}\]

We will apply each of these kernels to the original image to get two images, one that has been processed with the \(\text{Sobel}_x\) kernel (known as the x-gradient image) and one that has been processed with the \(\text{Sobel}_y\) kernel (known as the y-gradient image). This is the same process as was done for the Gaussian kernel, HOWEVER the negative values in these kernels can cause errors if they are not the correct type. To avoid this, ensure that the image array and kernel array are float type.

data_array = np.array(data, dtype=float)

Note

Remember to pad the image BEFORE applying these kernels like was done in Section 12.2.1.

Combining the gradient images :

To combine these two images, we will go pixel by pixel and compute the gradient magnitude which we will set as the pixel value in the combined image :

\[ \text{gradient_magnitude} = \sqrt{gx^2+gy^2} \]

Where :

• \(gx\) is the pixel value in the x-gradient image.

• \(gy\) is the pixel value in the y-gradient image.

• \(\text{gradient_magnitude}\) is the corresponding pixel’s value in the combined image.

Note

This formula CAN result in a \(\text{gradient_magnitude}\) that exceeds 255, which is not allowed for a grayscale image. You will need to ensure that values above 255 are clipped down to 255.

Thresholding :

The last step of this filter is to set a pixel threshold. The combined output of the Sobel kernels will likely result in some pixels having a value that is not strictly black or white, this means that the pixel is somewhat of an edge pixel. To fix this, we set a threshold which will tell us the minimum value a pixel must have to be considered an edge.

Iterating through each pixel of the combined Sobel kernel image we apply the following logic :

\[\begin{split} \text{If pixel_value}~\ge~\text{threshold :}\\ \text{pixel_value}~ = 255\\\\ \text{If pixel_value}~<~\text{threshold :}\\ \text{pixel_value}~ = 0 \end{split}\]

Thresholding can have a major impact on the output image from the Sobel filter, and a poorly chosen value can completely disrupt the whole point of the filter in the first place. To showcase this lets look at the following outputs :

WITHOUT Thresholding :

Fig. 12.14 Sobel Filter Without Thresholding

Threshold value set to 15 :

Fig. 12.15 Sobel Filter Low Thresholding

Threshold value set to 240 :

Fig. 12.16 Sobel Filter High Thresholding

Threshold value set to 50 :

Fig. 12.17 Sobel Filter Good Thresholding

As we can see, low thresholding results in far too many pixels being classified as edges, high thresholding results in not enough pixels being classified as edges, and in both cases we lose most of the details that were present in the original image.

For the images that we will be trying to process, the traffic signs, the threshold value we found to be a good balance of edge detail across the board was 50.

Note

Threshold values are entirely dependent on the images that you are processing, so it is always best to find a value that best represents YOUR data set whenever using the Sobel Filter.

Writing the function :

You will now write a function sobel_filter that takes in the blurred grayscale image (blurred using the gaussian_filter from Section 12.2.1) and outputs a uint8 NumPy array of the Sobel filtered image. The function will need to :

1. Initialize the \(\text{Sobel}_x\) and \(\text{Sobel}_y\) kernels.

2. Compute the x-gradient and y-gradient images by applying the \(\text{Sobel}\) kernels.

• Remember to pad the image with zeros before applying the kernels

3. Combine the gradient images using the \(\text{gradient_magnitude}\) formula.

• Remember to clip values greater than 255

4. Use a threshold of 50 for each pixel in the combined image.

Organize your code to use functions that break up the task into manageable pieces. Use the files provided in the Table 12.6 to test your code.

Table 12.6 Image Files

Image File Name	Description
ref_col.png	A color image
ref_col_b.png	A grayscale image

Sample Output

Use the values in Table 12.7 below to test your program.

Table 12.7 Test Cases

Case	image_path
1	ref_col.png
2	ref_col_b.png

Ensure your program’s output matches the provided samples exactly. This includes all characters, white space, and punctuation. In the samples, user input is highlighted like this for clarity, but your program should not highlight user input in this way.

Case 1 Sample Output

$ python3 tp2_team_2_teamnumber.py Enter the path to the image file: ref_col.png

Fig. 12.18 Case_1_ref_col_edge.png

Case 2 Sample Output

$ python3 tp2_team_2_teamnumber.py Enter the path to the image file: ref_col_b.png

Fig. 12.19 Case_2_ref_col_b_edge.png

Table 12.8 Deliverables

Deliverables	Description
tp2_team_2_teamnumber.pdf	Flowchart(s) for this task.
tp2_team_2_teamnumber.py	Your completed Python code.