\[ \begin{align}\begin{aligned}\newcommand\blank{~\underline{\hspace{1.2cm}}~}\\% Bold symbols (vectors) \newcommand\bs[1]{\mathbf{#1}}\\% Poor man's siunitx \newcommand\unit[1]{\mathrm{#1}} \newcommand\num[1]{#1} \newcommand\qty[2]{#1~\unit{#2}}\\\newcommand\per{/} \newcommand\squared{{}^2} \newcommand\cubed{{}^3} % % Scale \newcommand\milli{\unit{m}} \newcommand\centi{\unit{c}} \newcommand\kilo{\unit{k}} \newcommand\mega{\unit{M}} % % Percent \newcommand\percent{\unit{\%}} % % Angle \newcommand\radian{\unit{rad}} \newcommand\degree{\unit{{}^\circ}} % % Time \newcommand\second{\unit{s}} \newcommand\s{\second} \newcommand\minute{\unit{min}} \newcommand\hour{\unit{h}} % % Distance \newcommand\meter{\unit{m}} \newcommand\m{\meter} \newcommand\inch{\unit{in}} \newcommand\foot{\unit{ft}} % % Force \newcommand\newton{\unit{N}} \newcommand\kip{\unit{kip}} % kilopound in "freedom" units - edit made by Sri % % Mass \newcommand\gram{\unit{g}} \newcommand\g{\gram} \newcommand\kilogram{\unit{kg}} \newcommand\kg{\kilogram} \newcommand\grain{\unit{grain}} \newcommand\ounce{\unit{oz}} % % Temperature \newcommand\kelvin{\unit{K}} \newcommand\K{\kelvin} \newcommand\celsius{\unit{{}^\circ C}} \newcommand\C{\celsius} \newcommand\fahrenheit{\unit{{}^\circ F}} \newcommand\F{\fahrenheit} % % Area \newcommand\sqft{\unit{sq\,\foot}} % square foot % % Volume \newcommand\liter{\unit{L}} \newcommand\gallon{\unit{gal}} % % Frequency \newcommand\hertz{\unit{Hz}} \newcommand\rpm{\unit{rpm}} % % Voltage \newcommand\volt{\unit{V}} \newcommand\V{\volt} \newcommand\millivolt{\milli\volt} \newcommand\mV{\milli\volt} \newcommand\kilovolt{\kilo\volt} \newcommand\kV{\kilo\volt} % % Current \newcommand\ampere{\unit{A}} \newcommand\A{\ampere} \newcommand\milliampereA{\milli\ampere} \newcommand\mA{\milli\ampere} \newcommand\kiloampereA{\kilo\ampere} \newcommand\kA{\kilo\ampere} % % Resistance \newcommand\ohm{\Omega} \newcommand\milliohm{\milli\ohm} \newcommand\kiloohm{\kilo\ohm} % correct SI spelling \newcommand\kilohm{\kilo\ohm} % "American" spelling used in siunitx \newcommand\megaohm{\mega\ohm} % correct SI spelling \newcommand\megohm{\mega\ohm} % "American" spelling used in siunitx % % Inductance \newcommand\henry{\unit{H}} \newcommand\H{\henry} \newcommand\millihenry{\milli\henry} \newcommand\mH{\milli\henry} % % Power \newcommand\watt{\unit{W}} \newcommand\W{\watt} \newcommand\milliwatt{\milli\watt} \newcommand\mW{\milli\watt} \newcommand\kilowatt{\kilo\watt} \newcommand\kW{\kilo\watt} % % Energy \newcommand\joule{\unit{J}} \newcommand\J{\joule} % % Composite units % % Torque \newcommand\ozin{\unit{\ounce}\,\unit{in}} \newcommand\newtonmeter{\unit{\newton\,\meter}} % % Pressure \newcommand\psf{\unit{psf}} % pounds per square foot \newcommand\pcf{\unit{pcf}} % pounds per cubic foot \newcommand\pascal{\unit{Pa}} \newcommand\Pa{\pascal} \newcommand\ksi{\unit{ksi}} % kilopound per square inch \newcommand\bar{\unit{bar}} \end{aligned}\end{align} \]

Dec 03, 2024 | 667 words | 7 min read

3.1.1. Materials

MS Excel - Descriptive Statistics

Descriptive statistics is a way to describe data using measures of central tendencies and variation (how spread out the data is). These allow us to make evidence-based decisions.

Basic Descriptors

Table 3.2 Deliverables

Function	Description	Formula
Count	The total number of data points in the set	=COUNT()
Minimum	Smallest value in the data set	=MIN()
Maximum	Largest value in the data set	=MAX()
Range	Differenence between the maximum and minimum values	=MAX() - MIN()

Note

The \(Range\) function is helpful in identifying outliers

Measures of Central Tendency

Table 3.3 Deliverables

Function	Description	Formula
Mean	Sum of all the data points divided by the total number of data points	=AVERAGE()
Meadian	Middle number of the data set*	=MEDIAN()
Mode	Most frequently occurring number	=MODE()
	If you expect one mode	=MODE.SNGL()
	If you expect multiple modes	=MODE.MULT()

Note

*- when data is listed from smallest to largest

The \(Mean\) function is sensitive to outliers. An outlier is a data point that is far away from the rest of the data

Data Spread

Table 3.4 Deliverables

Function	Description	Formula
Standard Deviation	The measure of the amount of variation in a data set	=STDEV.S()
	square root of the variance
Variance	Average of the squared difference of each data point from the mean	=VAR.S()
	standard deviation squared

Note

A low standard deviation suggests that the data points are close to the mean.

A high standard deviation suggests that the data points are more spread out.

Equations

Average

(3.1)\[\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i\]

Standard Deviation of the sample

(3.2)\[\sigma = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2}\]

Variance of the sample

(3.3)\[\sigma^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2\]

where,

\(\bar{x}\) is the average (mean) value of the sample.

\(x_i\) represents each individual data point.

\(n\) is the total number of data points.

\(\sigma\) represents the standard deviation of the sample.

\(\sigma^2\) represents the variance of the sample.

Note

Equation for standard deviation of the population

(3.4)\[\sigma = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i - \mu)^2}\]

Equation for variance of the population

(3.5)\[\sigma^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i - \mu)^2\]

where,

\(\mu\) is the average (mean) value of the population.

MS Excel - Histograms

Installing the Data Analysis ToolPak

Follow the steps below to install the Data Analysis ToolPak as an Add-in on your system.

Windows

1. From the File menu select Options (bottom left).

2. In the Options window, select Add-ins and then click on Go.

   

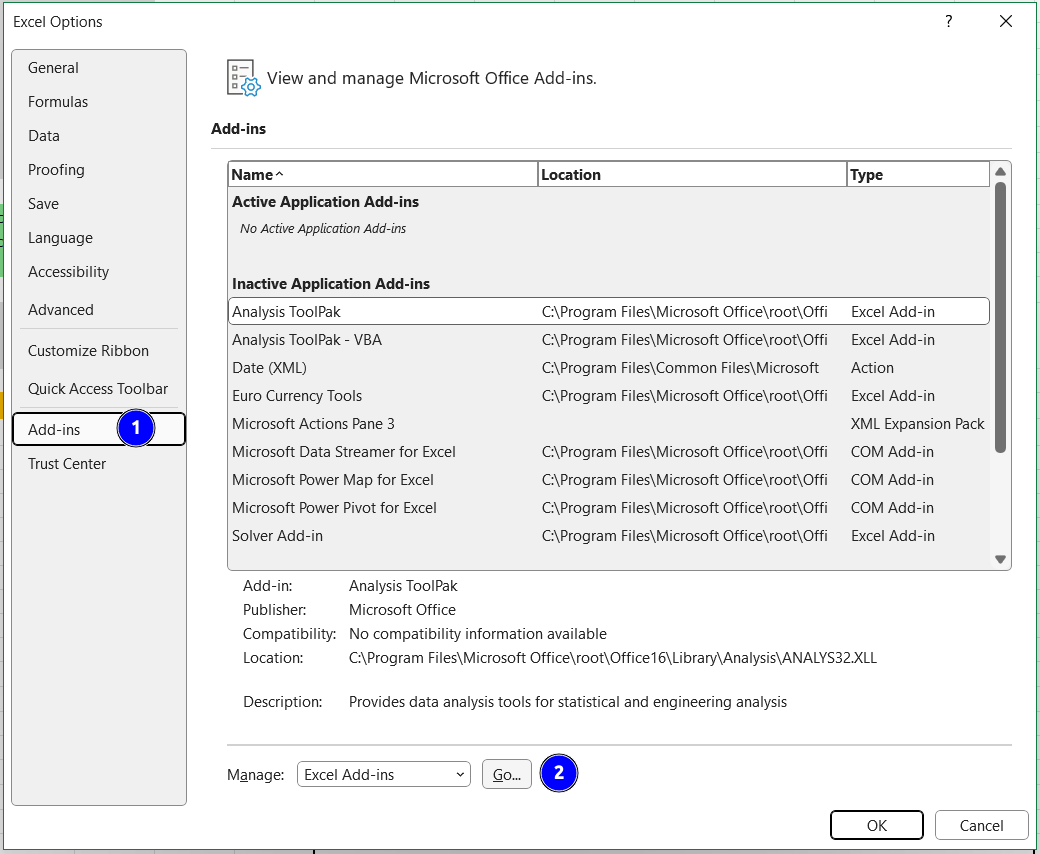
   Fig. 3.1 The MS Excel options menu.

3. In the Add-ins menu, select Analysis ToolPak and then click OK.

   

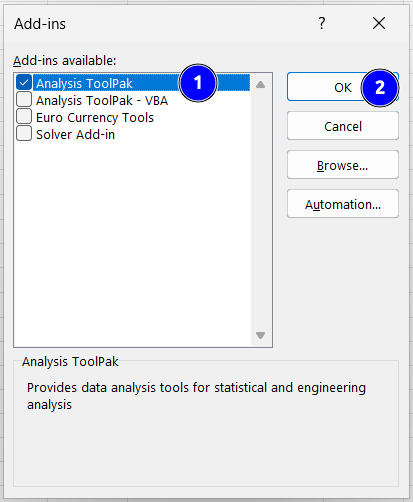
   Fig. 3.2 The MS Excel Add-ins menu.

4. Now you can find the Analysis ToolPak under the Data tab in the Analysis section of the ribbon.

   

   Fig. 3.3 The MS Excel ribbon with Analysis ToolPak installed.

mac OS

1. From the Tools menu select Excel Add-ins.

   

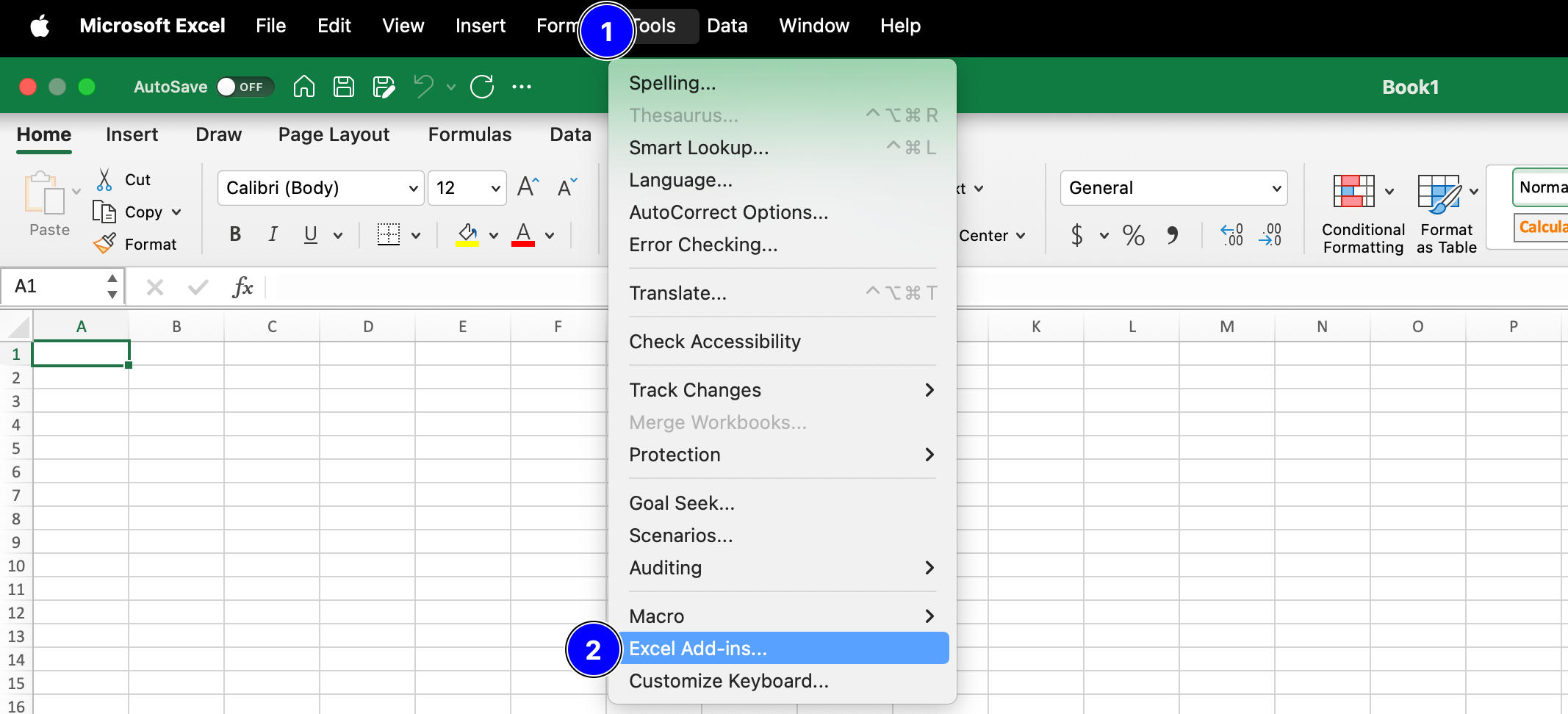
   Fig. 3.4 The MS Excel options menu.

2. In the Add-ins window, check the box next to Analysis ToolPak and then click on OK.

   

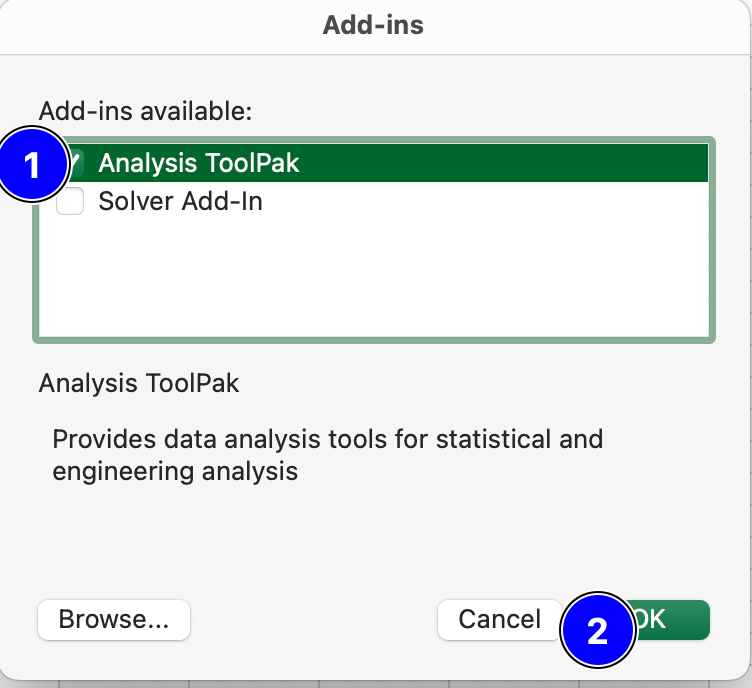
   Fig. 3.5 The MS Excel Add-ins menu.

3. Now you can launch the Analysis ToolPak by navigating to the Data tab and clicking on Data Analysis.

   

   Fig. 3.6 The MS Excel ribbon with Analysis ToolPak installed.

Creating a histogram using the Data Analysis ToolPak

Here is the example worksheet used in the above video - HistogramExample_Landfillwaste.xlsx

Note

A work through for both options above is provided here Excel_HistogramExample_FabricIgnition.xlsx.

Note

If a histogram displays continuous data, there should be no gap between your bins.

Basic Flowcharts

Click on this link to learn how to create a basic flowchart in MS Visio.

Click on this link to watch a video on how to create a basic flowchart in MS Visio.

Skewness

Skewness is a measure of a dataset’s symmetry (or lack of symmetry). MS Excel function is SKEW()

A perfectly symmetrical data set will have a skewness of 0 and is often known as a normal distribution. A skew less than zero (negative) has a long tail to the left. A skew greater than zero (positive) has a long tail to the right.

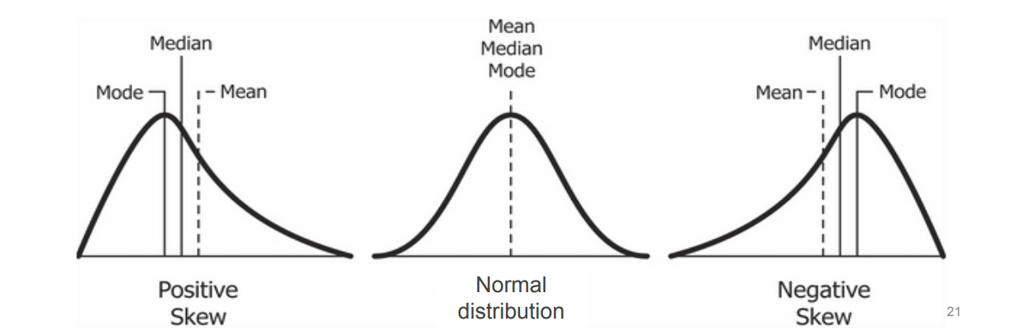
Fig. 3.7 Relationship between mean, median, mode with the skewness.

Note

Please note that the relationship between mean and median only serves as a rule of thumb for the skewness. If possible, you should always compute the skewness itself instead of relying on a rule of thumb. The skewness can be computed in MS Excel via the SKEW() function (which computes the adjusted Fisher-Pearson standardized moment coefficient). Read more about this here.

Kurtosis

Kurtosis is a measure of the peakedness and flatness of a distribution. MS Excel function is KURT().

Distributions with negative kurtosis exhibit tail data exceeding the tails of normal distribution. Distributions with positive kurtosis exhibit tail data that is generally less extreme than the tails of the normal distribution.

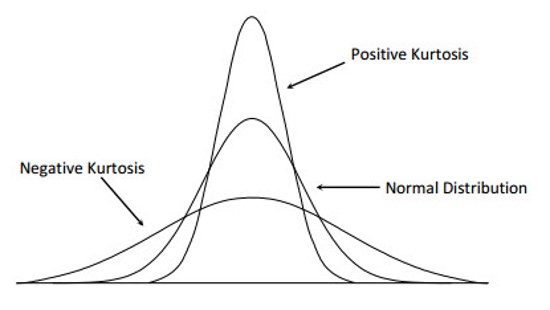
Fig. 3.8 Kurtosis Distribution.

Note

Skewness differentiates extreme values in one versus the other tail, kurtosis measures extreme values in either tail.